Research

My research activities are divided into different strands and projects. The publications are reported by subject area and project in descending temporal order.
The same information can be found on either my , my , or my profile.

Solving Linear Algebra problems is a core task in pretty much every Scientific challenge, from the numerical solution of partial differential equations to the new problems arising in the analysis of larger and larger sets of data. Moreover, we are fastly moving towards the use of exascale-enabled HPC platforms, thus we need to be capable of pushing our algorithms (and codes) to work efficiently in this environment. This first research line deals with this type of issue, and more specifically with the task of solving linear systems of equations, $$ A \mathbf{x} = \mathbf{b}, \qquad A \in \mathbb{R}^{N \times N}, \; \mathbf{x},\mathbf{b} \in \mathbb{R}^{N}, $$ in which $A$ is a large, $N \geq 10^9$, and sparse, number on non-zero entries proportional to $N$, matrix. The key instruments are here Krylov Subspace Methods, Geometric and Algebraic Multigrid preconditioners, and the application of update strategies to deal with more than one linear system.

Preconditioning for large and sparse linear systems

D'Ambra, P.; Durastante, F.; Filippone, S.; Massei, S.; Thomas, S.; Optimal Polynomial Smoothers for Parallel AMG. Submitted (2024).
D'Ambra, P.; Durastante, F.; Filippone, S.; PSCToolkit: solving sparse linear systems with a large number of GPUs. Submitted (2024).
Owen, H.; Lehmkuhl, O.; D'Ambra, P.; Durastante, F.; Filippone, S.; Alya towards Exascale: Algorithmic Scalability using PSCToolkit. J. Supercomput (2024). Open access
Bertaccini, D.; D'Ambra, P.; Durastante, F.; Filippone, S.; Why diffusion-based preconditioning of Richards equation works: spectral analysis and computational experiments at very large scale. (2023). Numer. Linear Algebra Appl.; e2523. Open access
D'Ambra, P.; Durastante, F.; Filippone, S.; Zikatanov, L.. Automatic coarsening in Algebraic Multigrid utilizing quality measures for matching-based aggregations. Comput. Math. Appl. 144 (2023), 290-305. MR4615364 Open access
D'Ambra, P.; Durastante, F.; Ferdous, S.M.; Filippone, S.; Halappanavar, M.; Pothen A.. AMG Preconditioners based on Parallel Hybrid Coarsening and Multi-objective Graph Matching. (2023). 31st Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP), Naples, Italy, 2023, pp. 59-67.
P. D'Ambra; F. Durastante; S. Filippone; Parallel Sparse Computation Toolkit. Software Impacts 15 (2023), no. 100463. Open Access.
D'Ambra, P.; Durastante, F.; Filippone, S.. AMG Preconditioners for Linear Solvers towards Extreme Scale. SIAM J. Sci. Comput. 43 (2021), no. 5, S679-S703. MR4331965
Bertaccini, D.; Durastante, F.. Iterative methods and preconditioning for large and sparse linear systems with applications. Monographs and Research Notes in Mathematics. CRC Press, Boca Raton, FL, 2018. xviii+353 pp. ISBN: 978-1-4987-6416-2 MR3793630
Bertaccini, D.; Donatelli, M.; Durastante, F.; Serra-Capizzano, S.. Optimizing a multigrid Runge-Kutta smoother for variable-coefficient convection-diffusion equations. Linear Algebra Appl. 533 (2017), 507--535. MR3695922
Bertaccini, D.; Durastante, F.. Interpolating preconditioners for the solution of sequence of linear systems. Comput. Math. Appl. 72 (2016), no. 4, 1118--1130. MR3529065

Fractional calculus is that subset of Analysis that studies the possibilities of defining differential operators of real or complex order. After the definition of such objects, the need to numerically approximate the solution of differential equations defined in terms of them immediately arises. The following papers deal with the efficient numerical solution of different formulations of such problems.

Fractional Differential Equations: Modeling, Discretization, and Numerical Solvers. Springer INdAM Series (SINDAMS, volume 50). Editors: A. Cardone, M. Donatelli, F. Durastante, R. Garrappa, M. Mazza, M. Popolizio. (2023). Pages XII, 146. ISBN: 978-981-19-7715-2. ISSN: 2281-518X.
Aceto, L.; Durastante, F.. Efficient computation of the Wright function and its applications to fractional diffusion-wave equations. ESAIM Math. Model. Numer. Anal. 56 (2022), no. 6, 2181--2196. MR4516169
Durastante, F.. Efficient solution of time-fractional differential equations with a new adaptive multi-term discretization of the generalized Caputo-Dzherbashyan derivative. Calcolo 56 (2019), no. 4, Paper No. 36, 24 pp. MR4015149
Bertaccini, D.; Durastante, F.. Efficient preconditioner updates for semilinear space-time fractional reaction-diffusion equations. Structured matrices in numerical linear algebra, 285--302, Springer INdAM Ser., 30, Springer, Cham, 2019. MR3931580
Bertaccini, D.; Durastante, F. Block structured preconditioners in tensor form for the all-at-once solution of a finite volume fractional diffusion equation. Appl. Math. Lett. 95 (2019), 92--97. MR3936774
Bertaccini, D.; Durastante, F.. Limited memory block preconditioners for fast solution of fractional partial differential equations. J. Sci. Comput. 77 (2018), no. 2, 950--970. MR3860196
Bertaccini, D.; Durastante, F.. Solving mixed classical and fractional partial differential equations using short-memory principle and approximate inverses. Numer. Algorithms 74 (2017), no. 4, 1061--1082. MR3626328

Numerical treatment of Fractional Differential Equations

Numerical optimal control theory is a part of numerical optimization that deals with the problem of finding a control for either a boundary value problem or a dynamical system over a period of time in such a way that an objective function is minimized/maximized. The prototypical problem of this type has the form $$ (y^*,u^*) = \arg\min_{u \in \mathcal{U}} J(y,u) = \frac{1}{2}\|y - y_z\|_2^2 + \frac{\lambda}{2} \| u \|_2^2, \text{ s.t. } e(y,u) = 0,$$ where $\mathcal{U}$ is a function space containing the admissible controls, $y_z$ a target state, and $e(y,u)=0$ a boundary value problem that the quantities $y$ and $u$ have to satisfy. The numerical solution of such a problem is challenging in many ways, it mixes together optimization, differential, and linear algebra problems in a non-trivial way.

Numerical optimal control of Partial Differential Equations

Durastante, F.; Furci, I.. Spectral analysis of saddle-point matrices from optimization problems with elliptic PDE constraints. Electron. J. Linear Algebra 36 (2020), 773--798. MR4188673 Open Access.
Durastante, F.; Cipolla, S.. Fractional PDE constrained optimization: box and sparse constrained problems. Numerical methods for optimal control problems, 111--135, Springer INdAM Ser., 29, Springer, Cham, 2018. MR3889795
Cipolla, S.; Durastante, F.. Fractional PDE constrained optimization: an optimize-then-discretize approach with L-BFGS and approximate inverse preconditioning. Appl. Numer. Math. 123 (2018), 43--57. MR3711990

A matrix function is simply a function which maps a matrix to another matrix, indeed to maintain interesting properties one has to extend the concept of scalar function to a matrix in a clever way. If, e.g., $f$ is a function admitting a Taylor expansion with radius of convergence $r$, and $A$ is a matrix such $\|A\| < r$ for any compatible norm $\|\cdot\|$, then $f(A)$ can be defined as $$ f(A) = \sum_{j=0}^{+\infty} c_k A^k, $$ for $c_k$ the Taylor coefficients of $f$. Equivalently, if $A$ is diagonalizable, and $f$ is defined on the eigenvalues of $A$, then $$ f(A) = X f(\Lambda) X^{-1}, \qquad A = X \Lambda X^{-1}, \; f(\Lambda)_{i,i} = f(\lambda_i(A)), $$ and in several other ways for more general $A$ and $f$. In any case, one of the principal numerical task that one can face is the computation of Matrix-Function-vector products, i.e., $\mathbf{y} = f(A)\mathbf{x}$, for $A$ a large and sparse matrix. The following line of research deals with these kind of problems by different techniques, and for different purposes (solution of Fractional differential equations, network analysis, etc.).

Aceto, L.; Durastante, F.. Efficient computation of the sinc matrix function for the integration of second-order differential equations. Advances in Computational Mathematics 50 (6), 109 (2024).
Aceto, L.; Durastante, F.. Theoretical error estimates for computing the matrix logarithm by Padé-type approximants. Linear Multilinear Algebra (2024), 1-20.
Durastante, F.; Meini, B.. Stochastic $p$th root approximation of a stochastic matrix: A Riemannian optimization approach. SIAM J. Matrix Anal. Appl. 45 (2024), no. 2, 875--904. MR4734557
Bertaccini, D.; Durastante, F.. Computing function of large matrices by a preconditioned rational Krylov method. Numerical mathematics and advanced applications ENUMATH 2019, 343--351, Lect. Notes Comput. Sci. Eng., 139, Springer, Cham, [2021], 2021. MR4266513
Bertaccini, D.; Durastante, F. Computing functions of very large matrices with small TT/QTT ranks by quadrature formulas. J. Comput. Appl. Math. 370 (2020), 112663, 15 pp. MR4046619
Aceto, L.; Bertaccini, D.; Durastante, F.; Novati, P. Rational Krylov methods for functions of matrices with applications to fractional partial differential equations. J. Comput. Phys. 396 (2019), 470--482. MR3989621
Bertaccini, D.; Popolizio, M.; Durastante, F. Efficient approximation of functions of some large matrices by partial fraction expansions. Int. J. Comput. Math. 96 (2019), no. 9, 1799--1817. MR3960343

Matrix-Functions

Network science is the study of complex networks that are nothing more than graphs that are both not random and not structured, e.g., one usually does not consider Cayley graphs encoding the structure of an abstract group. Examples are telecommunication networks, computer networks, biological networks, social networks, and many others. In each case, every actor is represented by a vertex of the graph and their connections as an edge. My interest in this field lies both in the modeling and the computational aspects, specifically in the task of extracting information on the networked phenomena by looking at the topology of the graph.

Graphs and Network Science: Complex-Networks

Benzi, M.; Durastante, F.; Zigliotto, F. Modelling advection on distance-weighted directed networks. Submitted (2024).
Cipolla, S.; Durastante, F.; Meini, B. Enforcing Katz and PageRank Centrality Measures in Complex Networks. Submitted (2024).
Bini, D. A.; Durastante, F.; Kim, S.; Meini, B. On Kemeny's constant and stochastic complement. Linear Algebra Appl. 703 (2024), 137-162. MR4797227 Open access
Bertaccini, D.; Durastante, F. Nonlocal diffusion of variable order on complex networks. Int. J. Comput. Math. Comput. Syst. Theory 7 (2022), no. 3, 172--191. MR4483942
Bianchi, D.; Donatelli, M.; Durastante, F.; Mazza, M.. Compatibility, embedding and regularization of non-local random walks on graphs. J. Math. Anal. Appl. 511 (2022), no. 1, Paper No. 126020, 30 pp. MR4379318
Arrigo, F.; Durastante, F.. Mittag–Leffler Functions and their Applications in Network Science. SIAM J. Matrix Anal. Appl. 42 (2021), no. 4, 1581--1601. MR4340667
Cipolla, S.; Durastante, F.; Tudisco, F.. Nonlocal pagerank. ESAIM Math. Model. Numer. Anal. 55 (2021), no. 1, 77--97. MR4216832
Benzi, M.; Bertaccini, D.; Durastante, F.; Simunec, I.. Non-local network dynamics via fractional graph Laplacians. J. Complex Netw. 8 (2020), no. 3, cnaa017, 29 pp. MR4130854

Inverse problems are involved in the task of inferring the parameters of the model from a set of (possibly noisy) measurements requires. These types of problems can be difficult to solve for several reasons, e.g., one could be dealing with a lack of unicity, that is: different values of parameters are consistent with the measurement, and discovering the parameters may be challenging from the computational point of view. I have done some work in using linear algebra techniques for a particular type of inverse problem that is image denoise and deblurring, that is the process of removing blurring artifacts and noise from images (e.g., somebody shook the camera while we were taking the photo).

Cipolla, S.; Donatelli, M.; Durastante, F.. Regularization of Inverse Problems by an Approximate Matrix–Function Technique. Numer. Algorithms 88 (2021), 1275-1308. DOI. 10.1007/s11075-021-01076-y.
Cipolla, S.; Di Fiore, C.; Durastante, F.; Zellini, P.. Regularizing properties of a class of matrices including the optimal and the superoptimal preconditioners. Numer. Linear Algebra Appl. 26 (2019), no. 2, e2225, 17 pp. MR3911025

Regularization and Inverse Problems

Mathematical methods play also a role in unexpected settings like archaeology. They enable the analysis and interpretation of data, making predictions, and gaining insights into quantitatives aspects. Statistical techniques are commonly employed to analyze large datasets, such as excavation records, artifact distributions, and survey data. These methods help archaeologists identify patterns, trends, and correlations, allowing them to make inferences about past human behaviors and societal structures. Mathematical modeling is also utilized to reconstruct ancient landscapes, simulate settlement patterns, and explore the dynamics of cultural change over time. The integration of mathematics into archaeological investigations enhances the accuracy, precision, and efficiency of research, contributing to a quantitative understanding of some aspects of history.

Mauro, C.; Durastante, F.. On the use of lights in nocturnal seafaring during Antiquity. (2024). Submitted.
Mauro, C.; Durastante, F.; Díaz-Sánchez, C.. A Light in the Dark: The Role of Coastal Lights in Night Navigation in Antiquity Journal of Eastern Mediterranean Archaeology and Heritage Studies (2023), Accepted
Mauro, C.; Durastante, F.. Nocturnal Seafaring: the Reduction of Visibility at Night and its Impact on Ancient Mediterranean Seafaring. A Study Based on 8-4th Centuries BC Evidence Journal of Maritime Archaeology, (2024), 1-19 pp. Open access
Mauro, C.; Durastante, F.. Evaluating visibility at sea: Instrumental data and historical nautical records. Mount Etna from the Calabrian Ionian coast (Italy). The Journal of Island and Coastal Archaeology, 17.1 (2022), 21-42 pp.

Applications, intersections, contaminations

Membership in scientific societies

Istituto Nazionale di Alta Matematica (INdAM) - Gruppo Nazionale di Calcolo Scientifico (GNCS).
Società Italiana di Matematica Applicata e Industriale (SIMAI).
Society of Industrial and Applied Mathematics (SIAM) - Activity group in Linear Algebra.
International Linear Algebra Society (ILAS).
Unione Matematica Italiana (UMI).
ACM: Association for Computing Machinery.

Collaboration Network

Most of the work described here has been done with several collaborators. I am always working on expanding my network of collaborators by looking for people to do interesting things with.

Bibliometric indexes

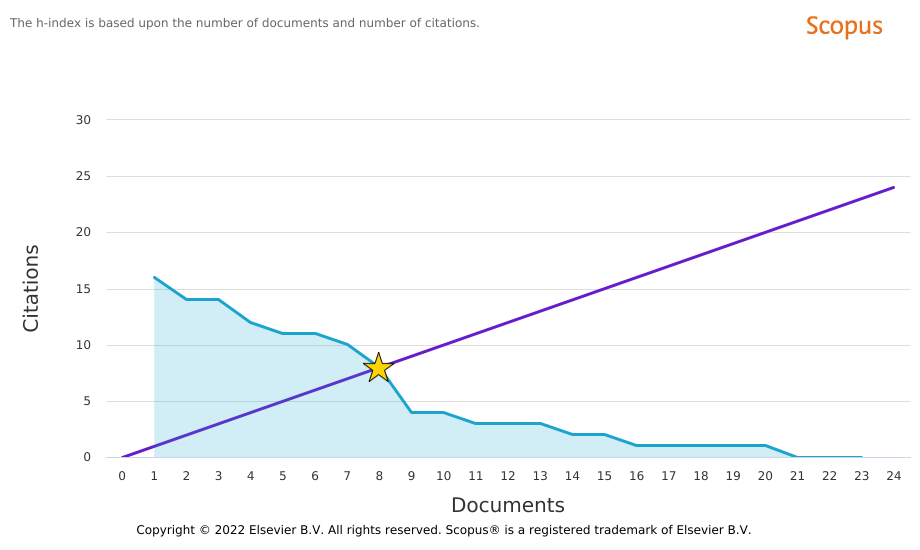
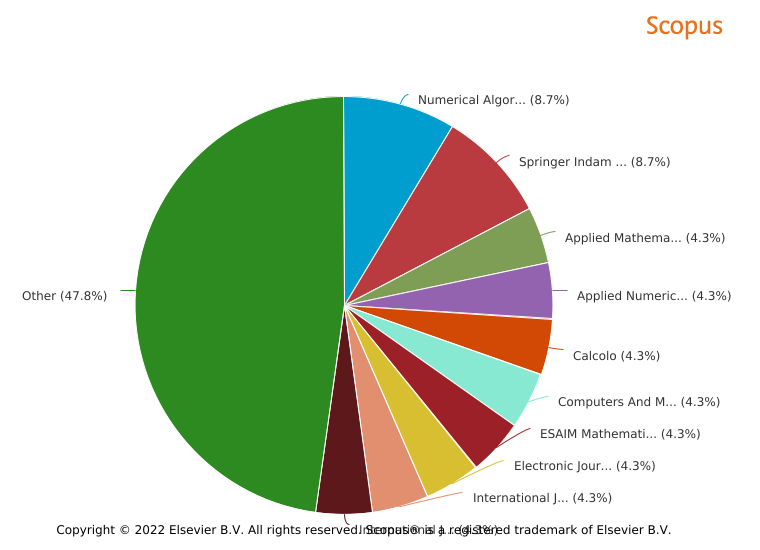
Not everything that counts can be counted, and not everything that can be counted counts.


(Scopus) H-Index: 9	(Scopus) Subject Areas

Editorial Work

I serve as editor for:

Computational and Applied Mathematics (Comput. Appl. Math.)
Journal of Mathematical Modeling (J. Math. Model.)

I have been part of the

AD/AE The 7th Annual Parallel Applications Workshop, Alternatives To MPI+X Sunday, November 17, 2024 held in conjunction with SuperComputing 17-22 November 2024, Atlanta.
AD/AE Appendices Process & Badges committee for the I Am HPC International Conference for High Performance Computing, Networking, Storage, and Analysis; Denver, Colorado November 12-17, 2023.
Member of the Program Committee for the 9th International Conference on Scale Space and Variational Methods in Computer Vision May 21-25 2023, Sardinia - Italy

I have served as reviewer for manuscripts submitted to the following journals.